Trim Hex Anagrams

As Martin Gardner fans new and old gear up to attend or host centennial Celebration of Mind events on or around 21 October 2014, including a special screening of long-lost video footage of the legendary mathematics popularizer—at the MAA Carriage House, Washington, DC—we add to the celebrations with another round of card considerations spawned by his always entertaining writing.

Between 1977 and 1986, Martin penned 111 "puzzle tales" for his friend Isaac Asimov's Science Fiction Magazine. They all resurfaced in three collections, the first and last of which are much more well known than the middle one. His words in the foreword to one of these books apply equally to all of them:

Each chapter poses a problem answered in the First Answers section. The solution in turn raises another problem that is solved in the Second Answers section. This may suggest a third question, and in several instances there is a fourth.... Many of the problems lead into nontrivial regions of mathematics and science.

As a result, a quick glance through any of these volumes soon suggests interesting things to explore with a deck of cards.

      

The first puzzle tale collection was Science Fiction Puzzle Tales (Potter, 1981), more familiar today in its MAA incarnation Mathematical Puzzle Tales from 2000. Just six months ago, "Postage Stamp Issue" (February 2014's Card Colm) drew inspiration from something found there.

Back in June 2005, "A Little Erdös/Szekeres Magic" took advantage of an observation from the final collection Riddles of the Sphinx and Other Mathematical Puzzle Tales (MAA, 1987). That two-person card effect actually first appeared in "(Smells like)Team spirit" from Mathematical Card Tricks (AMS Online, October 2000).

                      

This leaves the comparitively forgotten middle collection Puzzles From Other Worlds: Fantastical Brainteasers from Isaac Asimov's Science Fiction Magazine (Vintage, 1984), issued with two different covers, which includes several topics perfectly suited to card implementations. (What a wonderful MAA reissue this would make!) Below, we merely skim the surface of possibilities suggested by one of its puzzles, in a later iteration in the book.

Considered Yet Given

Consider the magic hexagram below:


(The image here is borrowed from Harvey Heinz's Magic 9x5 Hexagrams.) It appears on page 75 of Puzzles From Other Worlds, and unlike magic squares, is unfamiliar to most audiences. This pattern is doubly magic: each five-number horizontal, vertical, or diagonal row has a sum of 46, whereas each pair of opposite vertices sums to 7.

On page 165, Martin reveals that he was the first to find it, in response to a challenge issued by Harold Reiter in Mathematics Teacher in March 1983. He also found its "complement in 20"—obtained by subtracting each entry from 20—which has magic sum 54. The Heinz link above reveals that more have been discovered since, although far fewer than 57 varieties.

Note that 46 + 7 = 53, which is one more than the number of cards in a full deck. By taking advantage of an idea used in "A Magic Timepiece Influenced By Martin Gardner" (October 2007's Card Colm), we can put all of this to work.

Fan the faces of a jumbled-looking stack of 19 small index cards, on which the numbers 1 to 19 have been written, and deal them out face down on a large table into the above pattern. Turn away and ask for any five-card row or diagonal to be selected, and left in place. Have the remaining cards gathered up and set aside (the technical term for this is "destroying evidence").

Turn back. Quietly note to yourself if the selected row or diagonal includes the central 13 or not. If it doesn't, simply ask that the five index cards be turned over and their numbers added; the total will be 46. Indicate a deck of playing cards sitting on top of a folded page on the corner of the table, and have the person who selected the index cards count down to the 46th playing card. You wrote its value and suit on the page earlier before you folded it, so when the 46th card is arrived at, you can have the paper opened to confirm that it was totally predictable.

If the selected index cards include the central one, you can have even more fun. Pick them up, mix them a little, and hand them out. Ask for the total or the total of the two smallest numbers. (The mixing is to hide the fact that the two smallest numbers are always at each end of the row.) Either 46 or 7 will be reported. If 46, proceed as before, but if 7, hand over the 52-card deck face up and request that the 7th card from the deck face be located, as you mix in the other three index cards in with the rest. The card arrived at is the same as the 46th one from the other end, and hence will match the written prediction.

Here's a less cluttered magic hexagram, which is a type of magic star; it has magic constant 26 for sums of four values in a row.


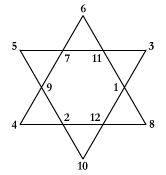
(The image is from from Wikipedia.) This too can be put to magic use, in a predictable way, one might say. This time, the intial display could consist of any Ace to Queen from a deck, with the forced or predictable card being 26 card from the top of the rest of the deck.

Electric Solvents

The hexagrams above had their summands at vertices. Another type has it summands in its cells. Consider the (unique) magic hexagrams below: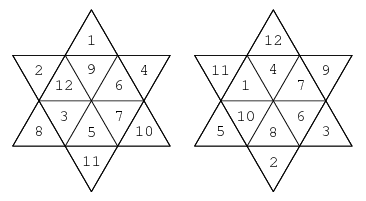


(from Weisstein, Eric W. "Magic Hexagram," MathWorld–A Wolfram Web Resource http://mathworld.wolfram.com/MagicHexagram.html)

Each (multicell) row or diagonal in the hexagram on the left sums to 33, and each corresponding row or diagonal in the hexagram on the right sums to 32. Note that these hexagrams are complementary: given one, the other may be obtained by subtracting its entries from 13. Using an idea implemented in "Sixy Alpha Omegas" (August 2007's Card Colm), we can fudge the 32/33 coincidence to magical effect as follows.

Draw two large blank hexagrams of the type just displayed, in which each cell is large enough to house a playing card. Take out a black-backed deck and show the faces of the cards to demonstrate how "random" they are. Deal out face-down cards from left to right into the rows of one of the hexagram, working from top to bottom, to match the left hexagram depicted above. The deck has of course been set up, only the values (Jack = 11, and Queen = 12) matter, so use a random mix of suits. Next, deal the next dozen cards into the other blank hexagon to match a rotated version of the right hexagram depicted above. Explain that in a moment you will turn away while an audience member picks a row or diagonal from either hexagram of cards. Have a few cards turned over briefly in both hexagrams to "verify" that they are different and unrelated.

Turn away and ask for any five-card row or diagonal to be selected, in either hexagram. Once again, have the rest of the cards gathered up and set aside. Now, have the values of the five chosen cards summed. From a red-backed deck that's been sitting in plain view all along have that number of cards dealt to the table. If 32 cards have been dealt, say, "The next card is yours," whereas if 33 cards have been dealt, say, "The last card is yours." Ask what it is, and have a prediction envelope—also on display from the outset—opened to confirm that you foresaw the outcome, value and suit. All that needs to be done to get this right is to start by jotting down the name of the card originally 33rd from the top.

Celebrations of Mind

John Peterson has written that "when Isaac Asimov was asked whom he thought was the most intelligent person on earth, he answered without hesitation, 'Martin Gardner.'" Centennial celebrations this autumn for this prolific and far-ranging author include numerous special articles and tributes. There's a wealth of Mathematics, Magic, & Mystery to explore at the associated Mathematics Awareness Month site too.

"Trim Hex Anagrams" is an anagram of "Martin's Hexagram." So is "Arrange Maths Mix". (There's another mirthful one we can't print here.) "Considered Yet Given" is one of a huge number of anagrams of "Distroying Evidence," and "Electric Solvents" is an anagram of "Cells Not Vertices."