We also salute an extremely prolific writer and top notch communicator of mathematics, with something brand new—courtesy of an old friend of his—that we are confident Martin would have found quite delightful.
What follows also makes a great Halloween Trick and Treat.
In the past month or so, fans new and old of Martin's written legacy have been attending and hosting Celebration of Mind events, all over the world, to mark the 21 October 2014 centennial of his birth. More events will take place from now till the end of the year.
Why not grab a deck of cards and a few receptive people, and try out out the first effect below, or one of the dozens from earlier? (The period 2004–2011 is documented here.) Please register here so we know where and when Martin is being honored.
Donkey Wontons





Next, gather up those cards, recombine them with the others, and place a second set of some of the five face down on the table. Again, make a true statement about each of them, asking if the card picked is one of those now on the table.
Should it be possible to tell which card was picked, if both questions were answered truthfully? First instincts suggest that two Yes/No answers can distinguish any one card from four, but perhaps not from five. However, one needs to consider the kinds of statements made about the cards placed on the table, as well as how many cards are involved each time.
For instance, imagine that two cards are placed on the table the first time, and it's correctly claimed, "The first is even-valued, and the second is 4 or higher." When the spectator is asked if the selected card is present, the answer is an unambiguous "No" provided that the selected card was the Ace or 3. However, if that card was the 2, 4 or 5, the spectator doesn't know for sure, and the only honest answer is, "I Don't Know."
It seems that we need to broaden our horizons and accept three types of answer: Yes, No, and I Don't Know, the last being equivalent to Maybe. This means that, after asking the usual question about two displays of face-down subsets of the original five cards, about which certain statements were made, there are nine possible combinations of answers that could be truthfully given. Presumably this is sufficient to narrow which one of the five cards was the one selected, if appropriate cards were displayed and appropriate statements made.
At first glance, it's tempting to think that the "I Don't Know" or "Maybe" option yields no information, but that's not the case at all. In the example above, for instance, such an answer tells us that the selected card was definitely the 2, 3 or 5. From there, one more clever "display and declare" decision, which we henceforth refer to as a query, should narrow down the selection to a single card. Such adaptive querying, where the second one depends on the answer received the first time around, is indeed possible every time.
True Thrill Alert
Let's be more ambitious, and seek an approach that uses two pre-determined queries that will be used in all cases.
In addition, let's relax the assumption that the spectator is guaranteed to be a truth teller. Perhaps the spectator is a compulsive liar instead. We have strayed into the realm of ternary logic, where we agree that the negation of Yes, No, and Maybe, are, respectively, No, Yes and again Maybe. (It's one of these latter answers that a liar would unhesitatingly give.)
This seems a tall order. We seek two queries which will be asked of a spectator, who could be either a consistent truth teller or a consistent liar, such that the answers received will permit the certain identification of the selected card.
This whole conundrum, and the surprisingly simple solution presented below, comes to us (and now to you) courtesy of mathematician and puzzle master Jerry Farrell, who was kind enough to share it as part of the Martin Gardner CentennialCelebrations.
Here are two queries that work in all cases. Remember all cards are displayed face down.
Query 1. The 5 is placed on the table, and beside it either the Ace or 3. The statement made reflects this perfectly "The first card is the 5 and the last one is also odd-valued."The ternary tree below tracks the possible answers to the two queries; note that the options are always taken in the order Yes, Maybe, No, from left to right. The best part about this scheme is that it works regardless of whether the spectator is a truth teller or liar.
Query 2. The 2 and 3 are placed on the table, followed by either the Ace or 5. The statement again reflects this reality: The first card is the 2, the next card is the 3, and the last one is odd-valued."
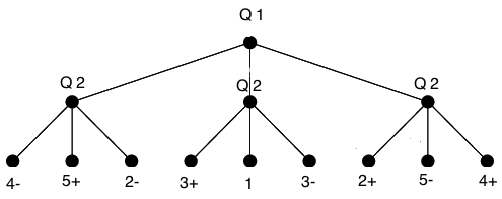
(tree courtesy of John Miller of Geom-e-Tree)
For instance, either two Yes or two No answers lead to the same conclusion: the selected card was the 4. Similarly, either a Yes or a No the first time followed by a "Maybe" the second time means that the card was the 5. But there's more, as the "+" or "-" signs attached to those values reveal: in most cases we can also say whether the spectator was lying or not. Note that "+" denotes truth telling and "-" indicates lying. The bottom line is, well, pleasantly symmetric. Also, this tree is easily memorized, avoiding the need for a crib sheet in performance.
Only in the case where the selected card was the Ace—corresponding to getting the answer "Maybe" twice—are we unsure whether we've been dealing with a truth teller or a liar all along. In all other cases, that information is revealed automatically, and it's prudent to announce the card picked while slipping in a casual comment such as, "I'm glad you told the truth" or "Despite your lies, I figured out your card."
If the spectator is lying, that person will probably then reveal that by denying that the selected card has been identified. Since that card was shown around earlier, you have nothing to worry about, the audience will be on your side. Furthermore, when the card was the Ace, a simple announcement of that in the form of the question, "Your card was the Ace, right?" will force both truth tellers and liars alike to self-identify.
In performance, when a participating spectator is decided on at the outset, stress that he or she must either lie all the way, or be totally truthful. Also, carefully explain the three options for each question asked, as well as the convention that the negation of Maybe is still Maybe, whether people agree with that logic or not!
Exercise 1: rework the above example with more interesting cards, such as four of a kind and a random fifth card, or a high straight, or even a killer straight flush.
Lying Reactor














These can be stacked at the top of the deck, in any order, and kept there throughout some sloppy false shuffling, before being dealt face down to the table and really mixed up. Finally, one is peeked at (and shown around). This gives the illusion that the cards used are totally random, which makes the outcome below all the more miraculous.
It turns out that with three carefully planned queries, posed to a truth teller or liar under the same conditions before, enough information will be gained to determine the selected card.
Here are three queries that work in all cases, as suggested by Jerry Farrell.
Query 1. The 2D, 4H, 6H, 8D, and X are placed on the table, where X is any card from the highest straight. The statement made reflects this, naming the first four cards and saying that the last one has value 10 or greater (Ace is high here).The resulting three-level tree, corresponding to the two-level one shown earlier, accounts for all 27 possible combinations of answers YYY, YYM, YYN, YMY, ..., NNN. The bottom line there is also elegantly symmetric, as can be checked. Even more delightfully, it points to these cards, in the order listed:
Query 2. The 2D, 7S, 9S, 10C, and QS are placed on the table, followed by any Heart not used already. The statement made names the first five cards, and indicates that the last one is a Heart.
Query 3. The 3C, 4H, 9S, and 10C are placed on the table, followed by any Red card not used already. The statement made names the first four cards, and says that the last one is Red.
Joker, 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K, Ace, K, Q, J, 10, 9, 8, 7, 6, 5, 4, 3, 2, JokerThat is to say, three Yes or three No answers guarantee the Joker, whereas two Yes answers followed by one Maybe points to the 2, as do two No answers followed by one Maybe, and so on.
Exercise 2: Sketch the three-level tree that ties all of this together, and practice decoding the various possibilities for the spectator's answers.
Exercise 3: Investigate the distribution of "+" and "-" in the extended bottom line above, does it work out as neat and tidy as it did in the earlier two-query case?
Exercise 4: Can the above be modified to switch the roles of the Ace and Joker? Would this make the Joker selection the only case where the truthfulness of the spectator would have to be teased out as suggested earlier, rather than being revealed automatically by the three answers received?
Exercise 5: Take it to the next level: if four queries are allowed, then from how many cards could a spectator be invited to choose one? Is it possible to devise queries leading to another symmetric bottom line in the resulting level-four tree?
These wonderful creations of Jerry Farrell's tie together several of Martin's favorite themes in mathematics and magic: logic, the interplay between numbers and language, the use of ternary methods, the convivial/contrary (or knight/knave) bystander motif, and the freedom to choice between lying or telling the truth in interactions with the performer. We are very grateful to Jerry for graciously allowing us to share these with everyone, via this column. As usual, we couldn't resist throwing in some anagrams, in the section headers.
Martin was a lifelong fan of wordplay, and contributed frequently to Word Ways: The Journal of Recreational Linguistics, a quarterly magazine now edited by Jerry Farrell, which was "established in 1968 at the behest of Martin Gardner." The Journalof Recreational Mathematics was also started, coincidentally in 1968, as a result of a suggestion of Martin's.
Don't forget the wise words of Persi Diaconis, "Pick up anything Martin Gardner wrote. You'll smile and learn something."
Thanks for Dana Richards for essential clarifications, and Vicki Powers for additional insight.
And finally, thank you for reading some or all of our ruminations here over the past decade.
"Certain Glory" and "Lying Reactor" (like "Lying Creator") are anagrams of "Ternary Logic." "Donkey Wontons" is an anagram of "Yes, No, Don't Know." Finally, "True Thrill Alert" is an anagram of "Truth Teller, Liar" (as is "Ultra Three Trill").
