Throughout his long and very productive life, mathematics popularizer
Martin Gardner was
intrigued by mathematical magic. He wrote extensively about it, and one of his
100+ books served as partial inspiration for the theme of 2014's
Mathematics Awareness Month. To mark
Martin's centennial year, recent
Card Colms (
Foregone Outset and
Postage Stamp Issue) have drawn on his writings to explore new card diversions,
and this month's romp continues that trend.
Entrant Vision
Consider a three-card game where a face-up Ace, 2, and 3 are on offer, and you
invite a friend to select any card.
If she picks the Ace, you pick the 2 and say, "2 is bigger than 1, so I win."
If she picks the 2, you pick the 3 and say, "3 is bigger than 2, so I win," and
of course, if she picks the 3, you pick the Ace and say, "Ace beats a 3, so I
win." Your friend wouldn't be too impressed, even if you only played one round
of this game. If multiple rounds were played, she'd probably complain that you
changed the rules as you went along. "The Ace can't be both high and low," she
might well cry, "You can't have it both ways." And yet we do have it both ways
when playing poker: both Ace, 2, 3, 4, 5, and 10, Jack, Queen, King, Ace are
considered to be straights, examples of rare five-card hands.
Wrap-arounds like that of course lead to cyclic arguments; the one above can be
summarized as 1 < 2 < 3 < 1 < ... ad infinitum. Cycles are hardly a new concept
in mathematics, though there is shock value in seeing them arise in the context
of strict inequalities, as we are much more familiar with transitive relations
than
non-transitive or
intransitive ones.
Some well-known games exhibit cyclic logic: for instance,
rock-paper-scissors.
Surprisingly, the three-card swindle above is essentially what's at the heart of
much more subtle paradoxes involving dice. We survey some of these before
switching our attention to playing cards.
Non-transitive phenomena of this stype first came to the public's attention via
Martin Gardner's
"Mathematical Games" column in
Scientific American, in December 1970.
There, he discussed a set of
four dice A, B,C, D, discovered by statistician Bradley Efron, for which which A > B > C > D
> A ..., in the sense that each die beats the next one listed with probability
2/3. See chapter 22 of Martin's
The Colossal Book of Mathematics
(Norton, 2001), or Ivars Peterson's "
Tricky Dice Revisited." As Gardner notes there, Karl Fulves published applications of
the Efron dice to card effects as early as 1971. Gardner provides several other
card incarnations.
Twisted Mortice
We're going to focus on sets of just three dice, for which the margin of victory
is generally smaller. There are sets of
three non-transitive dice close to ordinary dice for which the margin of
victory is very small indeed, but we prefer to focus on those associated with
English toy collector Tim Rowett of
Grand Illusions. He suggests colored dice on which are the following numbers:
Red = {1, 4, 4, 4, 4, 4},
Green = {2, 2, 2, 5, 5, 5},
Blue = {3, 3, 3, 3, 3, 6}.
Assume the dice are fair, meaning that each of the six sides comes up with the
same probability, and consider the game of rolling any two of the dice together,
over and over. There are the 6 x 6 = 36 equally likely outcomes. In the case of
Red and Green dice, the number on the Red one is less than the number on the
Green one 6 + 3 + 3 + 3 + 3 + 3 = 21 times. So 21/36 (or about 58%) of the time,
on average, Red loses to Green. Similarly, the Green die loses to the Blue one
6 + 6 + 6 + 3 = 21 out of 36 times, so again about 58% of the time, on average.
In conclusion, Green beats Red and Blue beats Green, on average.
The big surprise is that not only does Red beat Blue, on average, violating one's
deeply ingrained expectations of transitivity, it does so by an even larger
margin. Red in fact beats Blue 5 + 5 + 5 + 5 + 5 = 25 times out out 36, or about
or about 69% of the time, on average. Hence we arrive at the circular conclusion:
Red < Green < Blue < Red < ...
Note the similarity to the 1 < 2 < 3 < 1 < ... seen earlier, also bearing in mind
the lowest values on each of the three colored dice. Unlike in that case, which
required the Ace to be considered low in one context, and high in another, the
pairwise comparisons here seem quite legitimate. For the record, all three dice
have a mean of 21/6.
The standard way to take advantage these dice is a game where you invite a friend
to select any one of the dice, following which you pick another. Decide on a
fixed number of throws, such as a dozen, and roll the two selected dice that
number of times. If you've picked your die wisely, you should win more often
than your friend. Of course, if she picks the Red die, you pick the Green, if
she picks the Green you pick the Blue, whereas if she picks the Blue, you pick
the Red.
Amusing Strength
For a terrific kicker, play this a few times over, finally revealing your secret
technique, then invite your friend to try to beat you. This time, you offer to
select your die first, then have her pick one to beat yours. Once it's clear
that she has mastered the game, produce a second set of such dice, which she can
inspect to verify is identical to the first set. Announce that you'll continue
to go first, only this time each of you selects two dice of the same color. The
pairs are rolled, over and over, and the totals of the numbers obtained by each
of you is used to decide on the winner. The strategy she has just learned will
backfire badly on her: If you start by selecting the two Green dice, she will
confidently select the two Blue ones, only to find that on average she will lose.
Astonishingly, the new cycle of victory reverses the former one:
Red < Green < Blue < Red < ...
but
Red + Red > Green + Green > Blue + Blue > Red + Red > ...
Secondary Dice (Crayons Decide)
How might all of this work with cards, bearing in mind that a deck only has four
cards of each value? The basic idea is to replace each die with a packet of six
cards, from which one is randomly selected (with replacement) in between repeated
shuffles.
One possibility is to first double each of the values used for the dice, yielding
even numbers from 2 to 12 inclusive, then bump a few of them up by 1 to cut down
on excessive repetitions. This also neatly sidesteps the issue of whether Aces
are low or high.
Red = {2, 8, 8, 8, 9, 9},
Green = {4, 4, 5, 10, 10, Jack},
Blue = {6, 6, 7, 7, 7, Queen}.
Here the colors refer to the card backs for three decks. Red and Blue are
standard, find a deck with a different color to represent Green. Suits are
irrelevant. (Alternatively, you may opt to do all of this using cards from a
single deck, as long as you don't get confused as to which packet is which;
perhaps separate the packets on the table with large gaps, and use colored
markers or crayons as guides.)
Start with three such face-down packets of six cards, and ask a new friend to
pick one of the packets. You pick another one, remembering that Red < Green <
Blue < Red < ... as before. The cards in each selected packet are thoroughly
mixed and the rolling of dice is replaced by the random selection of one card
for each of you from each packet. Record whose card has the highest value,
replace the cards in their respective packets and mix them again, and continue.
With ten or twelve rounds, you should come out ahead on average, as in the dice
case.
Tawdry Codices
Here's another card incarnation with an additional element of randomization,
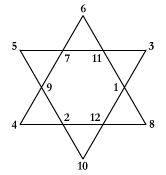
based on some well-known "magic square" dice. Consider the columns of the 3x3
magic square as shown:
2 7 6
9 5 1
4 3 8
Imagine a corresponding packet of face-down cards in mixed suits, running 2, 7,
6, 9, 5, Ace, 4, 3, 8, from the top down. Dealt from left to right, face up,
results in this display.









In practice, all dealing is done face down, and the columns overlap a little
vertically facilitating order-preserving pickups. Now gather the three columns
in any order–maintaining the card order within each column, and deal
out again into three piles, from left to right. Repeat over and over, until the
cards seem well mixed. Have a friend pick one column (pile) for himself, with
or without first looking at the card faces. Turn the other two piles over so
they are face up, and casually pick one of them for yourself. If you choose
wisely, you will on average win in a game of "best of a dozen" as before, where
this time the card packets have size three, simulating 3-sided dice. Once more,
your guiding light is 1 < 2 < 3 < 1 < ...: Simply scan the six visible card faces
for the Ace, 2, and 3. You will always see exactly two of those. The missing one
is in your friend's pile, so pick for yourself the pile that's "bigger and
better"—remembering that Aces are both low and high!
Why does this work? Certainly it's easy to check in the case when the three
piles are {2, 9, 4}, {7, 5, 3}, {6, 1, 8}, as they are at the outset: then
"Pile 2" (the one with the 2) beats "Pile 1" (the once with the Ace) about 56%
(=5/9) of the time on average, and "Pile 3" beats "Pile 2" and "Pile 1" beats
"Pile 3" by the same margin. This property of the columns of the standard 3x3
magic square (as displayed above) is well known, and is the basis for a set of
corresponding non-transitive 6-sided dice where each of the three key values is
used twice.
But what about the collection of the three columns in random order, in between
repeated dealings from left to right? Since there are six (=3!) ways in which
to gather the cards each time, one might expect as many possibilities for the
resulting three piles. It turns out that there are in essence only two things
that can happen. If the number of rounds of dealing and collecting is even, one
ends up with something equivalent to the initial display, from the perspective
of competing piles: the order in which the piles occur is irrelevant, as is the
internal card order within each pile. For instance, after four or six rounds of
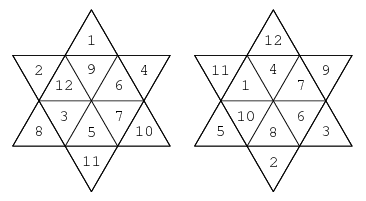
dealing and collecting, one could end up with:









While not a conventional magic square, it retains enough magical charm for our
purposes: It respects the partitioning of 1–9 into {1, 6, 8}, {2, 4, 9},
{3, 5, 7}, as does the result after any
even number of rounds of dealing
and collecting.
On the other hand, after any
odd number of rounds of dealing and
collecting, we get something like:









This is a representative of a class of equivalent arrays—the partitioning
of 1–9 into {1, 4, 9}, {2, 6, 7}, {3, 4, 8}—which are in turn
transposes of the kind we saw above after even numbers of rounds of dealing and
collecting.
Even better, the 1 < 2 < 3 < 1 < ... mantra again holds here for the new "Pile 1,"
"Pile 2," and "Pile 3"! That's why the stunt suggested works no matter how many
times the piles are dealt out and collected.
Indeed, the two partitions toggled between above are two of five existing for
1–9 that give rise to non-transitive dice, as documented in
The On-Line Encyclopedia of Integer Sequences entry
Sequence A121228.
There are many more variations on all of the above worth digging out. For instance,
M. Oskar van Deventer came up with a
set of seven dice such that for any two chosen dice there is a third one that beats them both.
"Recent Divinations" and "Card Intentions Vie" are two of many amusing
anagrams of "Non-transitive Dice," and "Entrant Vision" (like "Star Invention")
is an anagram of "Non-transitive." "Twisted Mortice" is an anagram of "Tim
Rowett's Dice," and "Amusing Strength" is an anagram of "Strange Sum Thing." "Secondary Dice" and "Crayons Decide" are anagrams of "Dicey Cards One," and
"Tawdry Codices" is an anagram of "Dicey Cards Two."